The Cartesian Product in miniKanren

I have become interested in modeling the Cartesian product as a relation in miniKanren. The Cartesian product is typically defined in terms of sets, but I will use lists since they are easier to work with in miniKanren. So the Cartesian product is a relation between three lists: l₁, l₂, and l₁×l₂.

(defrel (cartesian-producto l₁ l₂ l₁×l₂)

...)

The base case is straightforward. When l₁ is empty, then the product is empty. It is like multiplying by zero.

(defrel (cartesian-producto l₁ l₂ l₁×l₂)

(conde ((== l₁ '()) (== l₁×l₂ '()))

...))

The recursive case is more interesting. I always like to start by drawing a picture and annotating things that should be named in green. This helps me figure out the relationships.

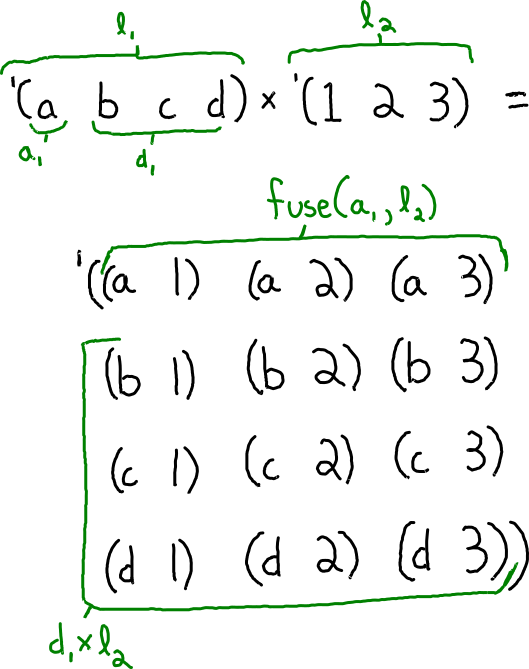
From this picture I can see that l₁ is nonempty, meaning it has a head a₁ and a tail d₁. That gives an opportunity for recurring on d₁×l₂. Finally, to get the entirety of l₁×l₂ I need to somehow "fuse" a₁ onto each element of l₂ and append it to d₁×l₂.

(defrel (cartesian-producto l₁ l₂ l₁×l₂)

(conde ((== l₁ '()) (== l₁×l₂ '()))

((fresh (a₁ d₁ d₁×l₂ fusion)

(== l₁ `(,a₁ . ,d₁))

(fuseo a₁ l₂ fusion)

(appendo fusion d₁×l₂ l₁×l₂)

(cartesian-producto d₁ l₂ d₁×l₂)))))

(defrel (fuseo sym l o)

(conde ((== l '()) (== o '()))

((fresh (a d rec)

(== l `(,a . ,d))

(== o `((,sym ,a) . ,rec))

(fuseo sym d rec)))))

(defrel (appendo l r o)

(conde ((== l '()) (== r o))

((fresh (a d rec)

(== l `(,a . ,d))

(== o `(,a . ,rec))

(appendo d r rec)))))

Let’s see if cartesian-producto can be run forwards:

For all my queries so far, I know that an answer exists and I’m asking miniKanren to find it. Let’s see if it can handle queries where there is no correct answer:

> (run 1 (q) (cartesian-producto '(a b c) '(1 2 3) '()))

'()

It correctly identified that that the cross product of '(a b c) and '(d e f) cannot be the empty list. Here is a trickier test: is '((a 1) (b 2)) the cross product of two lists? Never. Let’s see if miniKanren can figure that out.

> (run 1 (l₁ l₂) (cartesian-producto l₁ l₂ '((a 1) (b 2))))

...

The query diverges! It should produce '() like before, but it loops forever instead. Let’s analyze why.

This query provides a ground version of l₁×l₂, but it leaves l₁ and l₂ fresh. Since we know that l₁×l₂ is nonempty, the first conde clause fails, and so l₁ must be nonempty too. But l₂ could still be empty, in which case fusion is empty, and so appendo immediately halts with d₁×l₂ being unified to l₁×l₂. Then it recurs on d₁, which is fresh since l₁ was fresh, '(), and d₁×l₂, which is really just l₁×l₂. It is a recursive call where nothing has changed, except that l₂ is ground as the empty list (but that was picked on purpose), so it would continue to call itself infinitely.

1 First Refactor

One way to fix the divergence to separate l₂ into its empty and nonempty cases. This ends up being pretty straightforward: the output is empty when l₂ is empty and so does not require recursion. And now l₂ needs to be nonempty in the recursive clause.

(defrel (cartesian-producto l₁ l₂ l₁×l₂)

(conde ((== l₁ '()) (== l₁×l₂ '()))

((== l₂ '()) (== l₁×l₂ '()))

((fresh (a₁ d₁ a₂ d₂ d₁×l₂ fusion)

(== l₁ `(,a₁ . ,d₁))

(== l₂ `(,a₂ . ,d₂))

(fuseo a₁ l₂ fusion)

(appendo fusion d₁×l₂ l₁×l₂)

(cartesian-producto d₁ l₂ d₁×l₂)))))

It still diverges! But I’m not surprised. cartesian-producto is a recursive relation which uses two other recursive relations: fuseo and appendo.

2 Second Refactor

Another refactor I can try is to both fuse and append at the same time, e.g.:

> (run 1 (q) (fuse-and-appendo 'x '(a b c) '((y d) (y e) (y f)) q))

'(((x a) (x b) (x c)

(y d) (y e) (y f)))

That way, cartesian-producto would not need the intermediate variable fusion.

(defrel (cartesian-producto l₁ l₂ l₁×l₂)

(conde ((== l₁ '()) (== l₁×l₂ '()))

((== l₂ '()) (== l₁×l₂ '()))

((fresh (a₁ d₁ a₂ d₂ d₁×l₂ fusion)

(== l₁ `(,a₁ . ,d₁))

(== l₂ `(,a₂ . ,d₂))

(fuse-and-appendo a₁ l₂ d₁×l₂ l₁×l₂)

(cartesian-producto d₁ l₂ d₁×l₂)))))

Here is the implementation of fuse-and-appendo:

(defrel (fuse-and-appendo sym l r o)

(conde ((== l '()) (== r o))

((fresh (a d rec)

(== l `(,a . ,d))

(== o `((,sym ,a) . ,rec))

(fuse-and-appendo sym d r rec)))))

It’s not always possible to define conjunction of two recursive relations as a singly-recursive relation, so it’s great when it works. The basis for this correctness-preserving transformation is a logical rule of inference shown here:

\frac{((p \land a) \lor (\neg p \land b)) \land ((p \land x) \lor (\neg p \land y))}{(p \land a \land x) \lor (\neg p \land b \land y)}

That did the trick! But notice that fuse-and-appendo allows l₂ to be empty, so both refactors are needed together to prevent divergence.